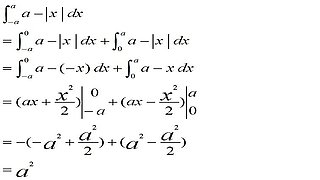微積分基本定理描述了微積分的兩個主要運算──微分和積分之間的關係。
定理的第一部分,稱為微積分第一基本定理,表明定積分可以用無窮多個原函數的任意一個來計算。這一部分有很多實際應用,這是因為它大大簡化了定積分的計算。
定理的第二部分,稱為微積分第二基本定理,表明不定積分是微分的逆運算。[1]這一部分定理的重要之處在於它保證了某連續函數的原函數的存在性。
該定理的一個特殊形式,首先由詹姆斯·格里高利(1638-1675)證明和出版。[2]定理的一般形式,則由艾薩克·巴羅完成證明。
微積分基本定理表明,一個變數在一段時間之內的無窮小變化之和,等於該變數的淨變化。